
Last but not least, if we found a prime number, we print it out. In the latter case, $isprime will have remained 1, and we have found a prime number. We repeat this until the test yields true or no more integers are left. On the other hand, if the test yields false, we execute the No branch, meaning we increment $i++ and move on to the next integer. If the test is true, we execute the Yes branch, let $isprime=0 and immediately quit the loop by executing the last command. The test $n % $i = 0 yields true if $n is divisible by $i. Inside the loop, you can see how we determine if $n is divisible. The chart below is an expanded version of the one above. In order to achieve this, starting from 2, we loop through all smaller numbers ($i) to see if $n is divisible by $i. Then we attempt to prove $n is not prime. Initially, we assume $n is prime, and therefore let $isprime=1. Inside the loop, for each number $n, we determine if it's prime or not. When that happens, we will have printed our list and the script ends. On each round, we increment $n++ until we have reached $max. We start from $n=2 and move towards 1000 one by one. Then we start looping through the numbers. In this script, we look for prime numbers in the range 2.1000.
#List of prime numbers to 1000 code#
The flow charts on this page were created by Visustin, a flow chart tool that converts source code to flow charts. In flow chart form, the algorithm looks like this: # See if $n is divisible by any smaller integer # Perl algorithm to print a list of prime numbers The printing usually happens on screen rather than on paper. As you run the script, it prints out all the prime numbers it finds. We use a brute-force approach to determine if a number is prime.īelow is our prime script in Perl. Simply go through all the numbers, check if they any of them is prime, and print it.

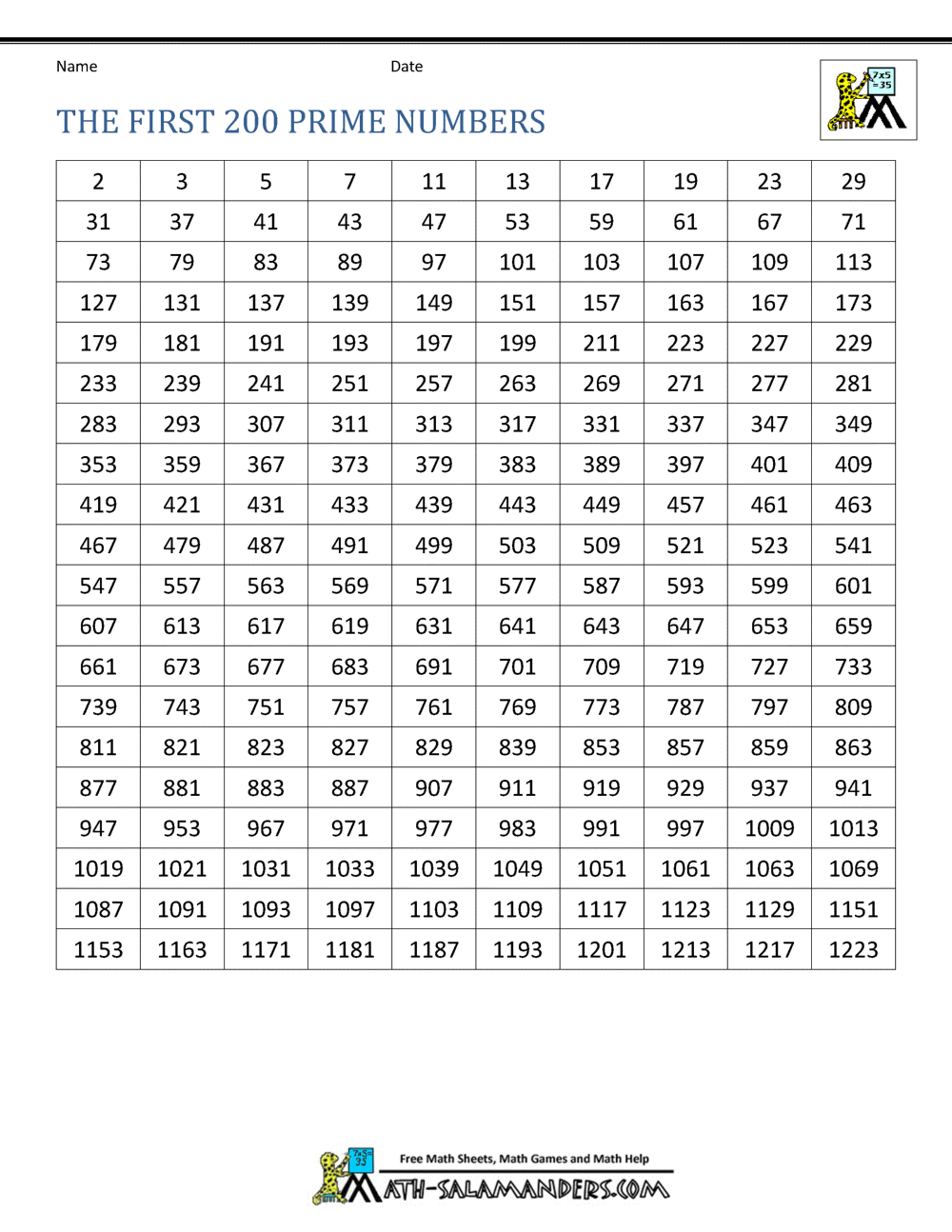
It's easy to print a list of prime numbers. The first few prime numbers are 2, 3, 5, 7, 11, 13 and 17. TheoryĪ prime number is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers.

Our algorithm is in Perl, but the principle is not language dependent. The algorithm lists all prime numbers in a given range. n is a natural number (including 0) in the definitions. More details are in the article for the name. Lists of primes by typeīelow are listed the first prime numbers of many named forms and types. A different computation found that there are 18,435,599,767,349,200,867,866 primes (roughly 2 ×10 22) below 10 24, if the Riemann hypothesis is true. There are known formulae to evaluate the prime-counting function (the number of primes below a given value) faster than computing the primes.
#List of prime numbers to 1000 verification#
The Goldbach conjecture verification project reports that it has computed all primes below 4×10 18. The following table lists the first 1000 primes, with 20 columns of consecutive primes in each of the 50 rows.


 0 kommentar(er)
0 kommentar(er)
